首都圏の高校入試より
こんにちは。藍住校からです。
さて、首都圏では入試が本格的に始まってきました。
今回はこちらからこの問題を引用してみます。
ちょっと難しめの問題ではありますが、チャレンジしてみましょう。
リンク先の東京新聞では今後入試問題が公開されていきますので
気になる方はチェックしましょう。
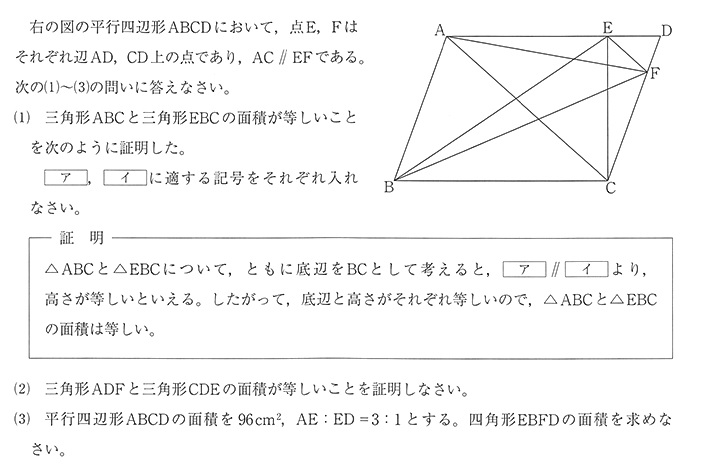
(1) AD//BC
(2) △ADF=△DEF+△AEF・・・①
△CDE=△DEF+△CEF・・・②
EF//ACより、△AEFと△CEFの高さは等しく、このとき底辺はEFで共通になっている。
したがって、△AEF=△CEFであるから、①、②より
△ADF=△CDEとなる。
(3) 四角形EBFDを平行四辺形ABCD-△AEB-△CFBとして考える。
AE:ED=3:1とEF//ACより、CF;FD=3:1
△AEBは△ABDの3/4である。また、△ABDは平行四辺形の1/2であるから、
△AEB=96×1/2×3/4=36
同様に△CFBは△BCDの3/4であり、△BCDは平行四辺形の1/2である。
よって△CFB=96×1/2×3/4=36
したがって、求める四角形EBFDの面積は
96-36-36=24
24㎠
徳島県の学習塾「伸学舎」「アイルセミナー」
088-669-6319 伸学舎 本部事務センター
088-693-1319 伸学舎 藍住校








